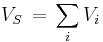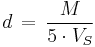Girolami method
The Girolami method,[1] named after Gregory Girolami, is a predictive method for estimating densities of pure liquid components at room temperature. The objective of this method is the simple prediction of the density and not high precision.
Contents |
Procedure
The method uses purely additive volume contributions for single atoms and additional correction factors for components with special functional groups which cause a volume contraction and therefore a higher density. The Girolami method can be described as a mixture of an atom and group contribution method.
Atom contributions
The method uses the following contributions for the different atoms:
| Element | Relative volume Vi |
|---|---|
| Hydrogen | 1 |
| Lithium to Fluorine | 2 |
| Sodium to Chlorine | 4 |
| Potassium to Bromine | 5 |
| Rubidium to Iodine | 7.5 |
| Cesium to Bismuth | 9 |
A scaled molecular volume is calculated by
and the density is derived by
with the molecular weight M. The scaling factor 5 is used to obtain the density in g·cm−3.
Group contribution
For some components Girolami found smaller volumes and higher densities than calculated solely by the atom contributions. For components with
- a hydroxylic function (Alcohols)
- a carboxylic function (Carboxylic acids)
- a primary or secondary amine function
- an amide group (incl. amides substituted at the nitrogen)
- a sulfoxide group
- a sulfone group
- a ring (non-condensed),
it is sufficient to add 10 % to the density obtained by the main equation. For sulfone groups it is necessary to use this factor twice (20 %).
Another specific case are condensed ring systems like Naphthalene. The density has to increased by 7.5 % for every ring; for Naphthalene the resulting factor would be 15 %.
If multiple corrections are needed their factors have to be added but not over 130 % in total.
Example calculation
| Component | M [g/mol] |
Volume VS | Corrections | Calculated density [g·cm−3] |
Exp. density [g·cm−3] |
|---|---|---|---|---|---|
| Cyclohexanol | 100 | (6×2)+(13×1)+(1×2)=26 | One ring and a hydroxylic group = 120 % | d=1.2*100/5×26=0.92 | 0.962 |
| Dimethylethylphosphine | 90 | (4×2)+(11×1)+(1×4)=23 | No corrections | d=90/5×23=0.78 | 0.76 |
| Ethylenediamine | 60 | (2×2)+(8×1)+(2×2)=16 | Two primary amine groups = 120 % | d=1.2×60/5×16=0.90 | 0.899 |
| Sulfolane | 120 | (4×2)+(8×1)+(2×2)+(1×4)=24 | One ring and two S=O bonds = 130 % | d=1.3×120/5×24=1.30 | 1.262 |
| 1-Bromonaphthalene | 207 | (10×2)+(7×1)+(1×5)=32 | Two condensed rings = 115 % | d=1,15×207/5×32=1.49 | 1.483 |
Quality
The author has given a mean quadratic error (RMS) of 0.049 g·cm−3 for 166 checked components. Only for two components (acetonitrile and dibromochloromethane) has an error greater than 0.1 g·cm −3 been found.
References
- ^ Gregory S. Girolami, A Simple "Back of the Envelope" Method for Estimating the Densities and Molecular Volume of Liquids and Volumes, J. of Chemical Education, 71(11), 962-964 (1994)